Collaborative Filtering
Fourth in a series on understanding FastAI.
- General context
- Data set
- Learning the Latent factors
- Creating the DataLoaders
- Collaborative Filtering from Scratch
General context
When we think about Netflix, we might have watched lots of movies that are science_fiction, action, horror etc. Netflix may not know these particular properties of the films you watched, but it would be able to see that other people that watched the same movies could watch other movies that you are not watching yet. By doing recommendation approach, Netflix can recommend us the contents of the movies that we have not watched before but relevant to what we liked.
This approach is called collaborative filtering. The key foundation idea is that of latent factors which decides what kinds of movies you want to watch.
from fastai.collab import *
from fastai.tabular.all import *
path = untar_data(URLs.ML_100k)
The information of the movies is structured as a table, where each column are respectively user, movie, rating and timestamp. Then, we need to indicate them when reading the file with pandas.
ratings = pd.read_csv(path/'u.data',delimiter='\t', header=None, names=['user','movie','rating','timestamp'])
ratings.head()
To have a more user-friendly interface, Figure below shows the same data cross-tabulated into a human-friendly table. As the example, the empty cells in the table are the things that we would like our model to fill in based on the other informations.

Basically, our objective is to recommend the movies to the people that might like them. In order to weight for each movie, how much the match of each category it is, we use the factos range between -1 and 1. For example, in oder to represent the movie The Last Skywalker for each category of science-fiction, action and old movies, we could use an array.
last_skywalker = np.array([0.98,0.9,-0.9])
Then we can score the interests of each user for each category by an array as well
user1 = np.array([0.8,0.6,-0.4])
Then, we calculate the matche between the combination which is a dot product:
(user1*last_skywalker).sum()
Since we dont know what the latent factors are, and we dont know how to score them for each user and movie, we should learn them.
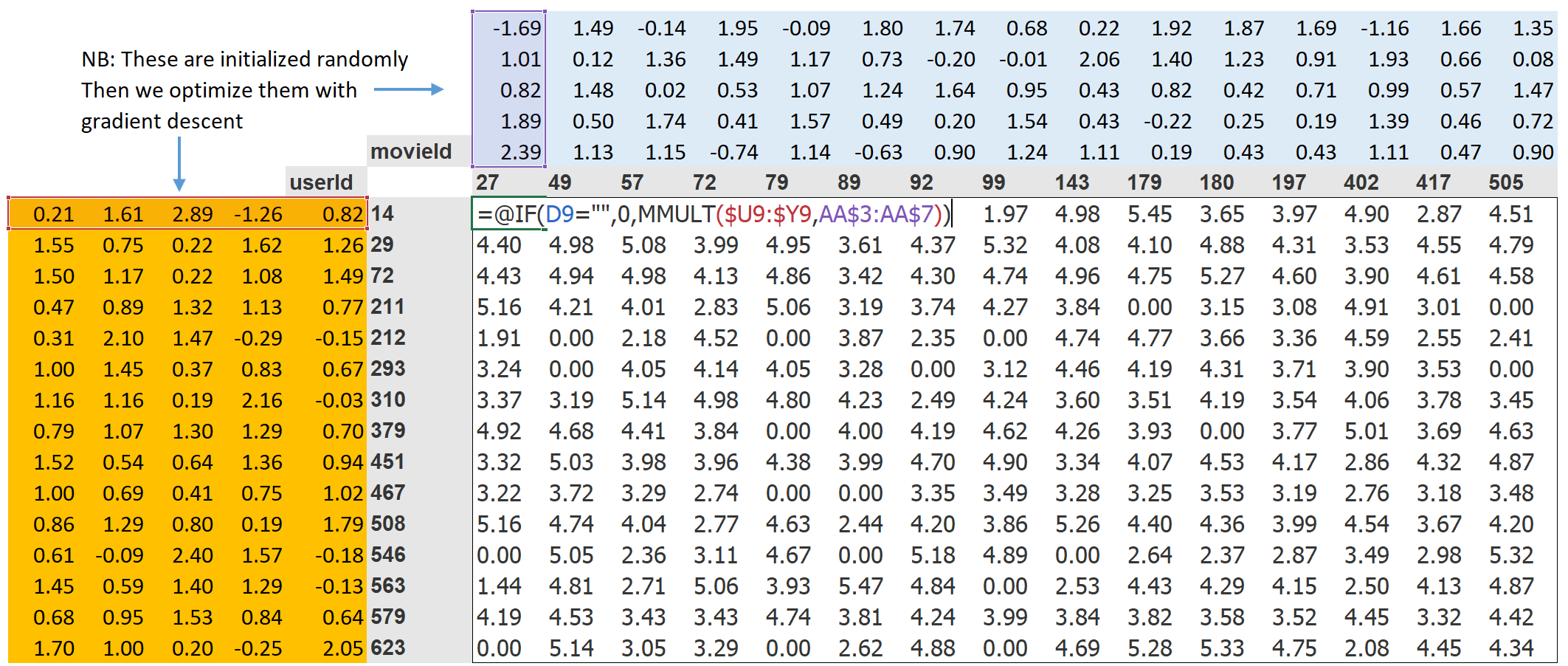
Step 1 of this approach is to randomly initialize some parameters. These parameters will be set as latent factors for each user and movie. For the illustrative purposes, we will use 5.
Step 2 of this approach is to calculate our predictions. By simply applying dot product of each movie with the user, by doing so, we can ontain a great match if an particular user likes a category of movies and the latent movies factor shows a lot of action.
Step 3 is to calculate our loss between our prediction and already obtained data.
With this in place, we can optimize our parameters using SGD, such as to minimize the loss.
movies = pd.read_csv(path/'u.item', delimiter='|', encoding='latin-1', usecols=(0,1), names=('movie','title'), header=None)
movies.head()
We will use merge the movies and our ratings
ratings = ratings.merge(movies)
ratings.head()
By using DataLoaders, it takes by default the first column fir user, the second column for the item and the third will be used for ratings.
dls = CollabDataLoaders.from_df(ratings,item_name='title',bs=64)
dls.show_batch()
Then, with Pytorch, we represent our movies and user latent factor tables as matrices
n_users = len(dls.classes['user'])
n_movies = len(dls.classes['title'])
n_factors=5
user_factors = torch.randn(n_users,n_factors)
movie_factors = torch.randn(n_movies,n_factors)
By looking up an index, we can find the factors of user and movie. It can be seen as a matrix product. By replacing our indices with one hot encoded vectors, we can represent it.
one_hot_3 = one_hot(3,n_users).float()
# latent factors of user 3
user_factors.t() @ one_hot_3
class DotProduct(Module):
def __init__(self,n_user,n_movies,n_factors):
self.user_factors = Embedding(n_users,n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
def forward(self,x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return (users*movies).sum(dim=1)
in this class, forward is a special Pytorch method name to notify us that a new Pytoch Module has just been created.
Then, we will create a Learner to optimize the parameters. We will use the plain Leaner class here:
model = DotProduct(n_users,n_movies,50)
learn = Learner(dls,model,loss_func=MSELossFlat())
learn.fit_one_cycle(5,5e-3)
To make the model slightly better, we can force those prediction between 0 and 5. Then, we need to apply sigmoid_range, like previous post.
class DotProduct(Module):
def __init__(self,n_user,n_movies,n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users,n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.y_range=y_range
def forward(self,x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
return sigmoid_range((users*movies).sum(dim=1),*self.y_range)
model = DotProduct(n_users,n_movies,50)
learn = Learner(dls,model,loss_func=MSELossFlat())
learn.fit_one_cycle(5,5e-3)
We will try to add bias to the weights and see what happens.
class DotProductBias(Module):
def __init__(self,n_user,n_movies,n_factors, y_range=(0,5.5)):
self.user_factors = Embedding(n_users,n_factors)
self.movie_factors = Embedding(n_movies, n_factors)
self.y_range=y_range
self.user_bias = Embedding(n_users,1)
self.movie_bias = Embedding(n_movies,1)
def forward(self,x):
users = self.user_factors(x[:,0])
movies = self.movie_factors(x[:,1])
res = (users*movies).sum(dim=1, keepdim=True)
res += self.user_bias(x[:,0]) + self.movie_bias(x[:,1])
return sigmoid_range((users*movies).sum(dim=1),*self.y_range)
model = DotProduct(n_users,n_movies,50)
learn = Learner(dls,model,loss_func=MSELossFlat())
learn.fit_one_cycle(5,5e-3)
In stead of being better, it becomes worse because it is overfitting very quickly. So we need to find a way to train with more epoch and avoid overfitting. To do that, we will use a regularization technique which is so-called weight decay
One possible way to reduce the overfitting effect is to reduce the capacity of the model which is basically how much space does it have to find answers. Weight decay or, L2 regularization, consists in adding of loss function the sum of all the weights squared. Then, to reduce the whole loss function, we need to reduce the weights. Then we reduce the likelihood of the big changes in the loss. As the results, the small changes in the weight can lead to the small changes in the loss. By doing that, we can prevent the model doing overfitting that happens with very sharp changes.
The downside of limiting the weights is that we limit the space of trying the possibilities. But it generalizes better
loss_with_wd = loss + wd * (parameters**2).sum()
model = DotProductBias(n_users,n_movies,50)
learn = Learner(dls,model,loss_func=MSELossFlat())
learn.fit_one_cycle(5,5e-3,wd=0.1)
By doing weight decay, as the results, we see the training loss increase but the validation loss slightly decrease. It means that the generalization works.
class T(Module):
def __init__(self): self.a = nn.Parameter(torch.ones(3))
By wrapping with nn.Parameter, Pytorch will assume that are parameters to be learned.
L(T().parameters())
Let's create a tensor as a parameter
def create_params(size):
return nn.Parameter(torch.zeros(*size).normal_(0, 0.01))
Let's use this to create DotProductBias again, but without Embedding:
class DotProductBias(Module):
def __init__(self, n_users, n_movies, n_factors, y_range=(0,5.5)):
self.user_factors = create_params([n_users, n_factors])
self.user_bias = create_params([n_users])
self.movie_factors = create_params([n_movies, n_factors])
self.movie_bias = create_params([n_movies])
self.y_range = y_range
def forward(self, x):
users = self.user_factors[x[:,0]]
movies = self.movie_factors[x[:,1]]
res = (users*movies).sum(dim=1)
res += self.user_bias[x[:,0]] + self.movie_bias[x[:,1]]
return sigmoid_range(res, *self.y_range)
Then we will train it again, we will see that there is no effect of embedding a layer.
model = DotProductBias(n_users, n_movies, 50)
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.1)
The structured above can be created using fastai.collab
learn = collab_learner(dls,n_factors=50,y_range=(0,5.5))
learn.fit_one_cycle(5,5e-3,wd=0.1)
Then, we can show the names of layers
learn.model
Now, we have succesfully trained a model.
To turn our architecture into a deep learning model, the first step is to take the results of the embedding lookup and concatenate those activations together. This gives us a matrix which we can then pass through linear layers and nonlinearities in the usual way.
Since we'll be concatenating the embeddings, rather than taking their dot product, the two embedding matrices can have different sizes (i.e., different numbers of latent factors). fastai has a function get_emb_sz that returns recommended sizes for embedding matrices for your data, based on a heuristic that fast.ai has found tends to work well in practice:
embs = get_emb_sz(dls)
class CollabNN(Module):
def __init__(self, user_sz, item_sz, y_range=(0,5.5), n_act=100):
self.user_factors = Embedding(*user_sz)
self.item_factors = Embedding(*item_sz)
self.layers = nn.Sequential(
nn.Linear(user_sz[1]+item_sz[1], n_act),
nn.ReLU(),
nn.Linear(n_act, 1))
self.y_range = y_range
def forward(self, x):
embs = self.user_factors(x[:,0]),self.item_factors(x[:,1])
x = self.layers(torch.cat(embs, dim=1))
return sigmoid_range(x, *self.y_range)
model = CollabNN(*embs)
CollabNN creates our Embedding layers in the same way as previous classes in this chapter, except that we now use the embs sizes. self.layers is identical to the mini-neural net we created in <forward, we apply the embeddings, concatenate the results, and pass this through the mini-neural net. Finally, we apply sigmoid_range as we have in previous models.</p>
</div>
</div>
</div>
learn = Learner(dls, model, loss_func=MSELossFlat())
learn.fit_one_cycle(5, 5e-3, wd=0.01)
learn = collab_learner(dls, use_nn=True, y_range=(0, 5.5), layers=[100,50])
learn.fit_one_cycle(5, 5e-3, wd=0.1)